Ein nichtlineares Reibmodell für die numerische Simulation reibungsbehafteter mechatronischer Systeme

ASIM 2002, 16. Symposium Simulationstechnik, Rostock, 10.-13. September 2002

Stephan Klotzbach
DMecS Development of Mechatronic Systems GmbH & Co. KG, Köln,
info@dmecs.de
www.dmecs.de

Hermann Henrichfreise
Cologne Laboratory of Mechatronics (CLM), Fachhochschule Köln,
info@clm-online.de
www.clm-online.de

Kurzfassung

Dieser Beitrag behandelt die Modellierung und Simulation von Reibung in mechatronischen Systemen. Aufbauend auf aus der Literatur bekannten Ansätzen wird ein mathematisches Modell für Reibung vorgestellt und auf dessen Implementierung in der Entwicklungsumgebung MATLAB/Simulink eingegangen. Dabei liegt ein besonderes Augenmerk auf der Einbeziehung lastabhängiger Reibung sowie auf der genauen numerischen Nachbildung aller Größen in den Zuständen Haften und Gleiten und der Übergänge zwischen diesen Reibungszuständen. Simulationsergebnisse für den Stick-Slip-Effekt und die lastabhängige Reibung zeigen die Funktionalität des Reibmodells. Das Modell kommt in einer Vielzahl von Anwendungen zum Einsatz. Einige Beispiele sind Aktoren für Lenkungen und Brake-by-wire sowie Kupplungen und Reifenmodelle.

1 Einleitung

Das Phänomen Reibung gewinnt bei der Entwicklung mechatronischer Systeme zunehmend an Bedeutung. Für regelungstechnische Systeme ist Reibung häufig ein unerwünschtes Phänomen, dessen Auswirkung auf Regelfehler von Antriebssystemen durch geeignete Maßnahmen zu kompensieren ist [1]. Für Kupplungen [2], Bremsen und Reifen ist Reibung dagegen ein erwünschtes Phänomen. In allen Fällen sind für eine Vorhersage der Auswirkungen von Reibung auf das Systemverhalten mit Hilfe der numerischen Simulation zuverlässige Modelle erforderlich. Diese Modelle müssen für die HIL-Simulation z.B. von Antriebssträngen oder Gesamtfahrzeugen zusätzlich echtzeitfähig sein.
Zum Thema Reibung gibt es eine Vielzahl von Veröffentlichungen. Einige grundlegende Arbeiten für die Beschreibung von Reibung aus mechatronischer Sicht sind mit [3] bis [8] gegeben. Die in [3] bis [5] angegebenen Modelle berücksichtigen dabei die in vielen realen Systemen auftretende Lastabhängigkeit der Reibung. Die in Kapitel 2 dargestellte Modellbildung führt die Ansätze aus [4] bis [7] zu einem Modell für die Simulation von Reibung zusammen. Dabei wird ein neuer Ansatz für die Lastabhängigkeit von Reibung vorgestellt. In Kapitel 3 wird kurz auf die programmtechnische Implementierung in der Entwicklungsumgebung MATLAB/Simulink eingegangen. Hier wird besonderer Wert auf die genaue numerische Nachbildung aller Größen in den Zuständen Haften und Gleiten sowie der Übergänge zwischen diesen Reibungszuständen gelegt. Das Ergebnis ist ein in einem weiten Anwendungsfeld einsetzbares, leicht parametrierbares Modell in Form eines Simulink-Subsystems.
Kapitel 4 belegt mit Simulationsergebnissen die Qualität des Reibmodells. Mit einer Zusammenfassung und Beispielen für den erfolgreichen Einsatz des Modells in Kapitel 5 schließt der Beitrag ab.

2 Modellbildung

Das nachfolgend beschriebene Modell für Reibung ist mit Bild 2.1 und den dargestellten Kraft- und Bewegungsgrößen leicht nachvollziehbar.

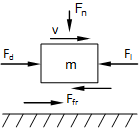
Bild 2.1: Bewegte Masse mit Reibung

Die Masse m bewege sich mit der Geschwindigkeit v relativ zu einer feststehenden Oberfläche. Auf die Masse wirke die antreibende Kraft Fd, die Lastkraft Fl sowie eine Normalkraft Fn. Die resultierende Reibkraft Ffr kann gemäß [4; 5] durch die Fallunterscheidung

paper_prev_DMecS_Reibung_paper_equation1

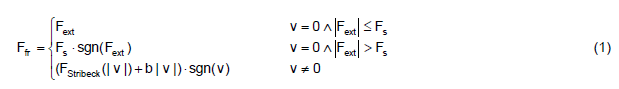
dargestellt werden. Darin beschreibt die erste Zeile die Reibkraft für den Zustand des Haftens. Die Reibkraft befindet sich im statischen Gleichgewicht mit der Summe Fext = Fd – Fl der äußeren antreibenden und verzögernden Kräfte. Dieser Zustand besteht für v = 0 solange der Betrag der Summe Fext die Losbrechkraft (statische Reibkraft) Fs nicht übersteigt. Übersteigt die Summe Fext die statische Reibkraft, geht die Masse vom Haften in das Gleiten über. In diesem Zustand des Losbrechens ist die Reibkraft gemäß der zweiten Zeile der Fallunterscheidung vom Betrag gleich der statischen Reibkraft, und ihr Vorzeichen ist durch das Vorzeichen von Fext gegeben. Schließlich beschreibt die dritte Zeile in Gleichung (1) die Reibkraft für den Zustand des Gleitens. In diesem Zustand ist die Reibkraft eine Funktion der Geschwindigkeit und ist der Bewegung der Masse entgegengerichtet. Sie setzt sich aus den Anteilen trockener Reibung und bei Vorliegen eines Schmierfilms geschwindigkeitsproportionaler viskoser Reibung mit dem Proportionalitätsfaktor b zusammen. Die trockene Reibung kann in Anlehnung an [4; 5] für v > 0 durch die Gleichung

beschrieben werden. Neu hinzukommende Größen sind die kinetische (Coulombsche) Reibkraft Fk und die Stribeck-Geschwindigkeit vStribeck. Letztere bestimmt den exponentiellen Übergang von Haft- zu Gleitreibung im Mischreibungsbereich. In diesem Bereich nehmen mit zunehmender Geschwindigkeit durch den Aufbau eines Schmierspaltes der Kontakt der Oberflächenrauhigkeiten und damit die Reibkraft ab. Der vorliegende Verlauf mit Mischreibung kennzeichnet die so genannte Stribeck-Reibung. Bild 2.2 zeigt die durch Gleichungen (1) und (2) beschriebene Reibkennlinie mit den zugehörigen Parametern.

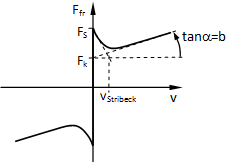
Bild 2.2: Reibkennlinie
Das bisher vorgestellte Reibmodell wird nun um lastabhängige Reibung erweitert. Lastabhängigkeit der Reibkraft liegt vor, wenn sich die Normalkraft Fn in Bild 2.1 mit der Lastkraft Fl erhöht. Der einfachste Ansatz, der praktisch für alle Getriebe mit konstanter Übersetzung gilt, ist ein proportionaler Zusammenhang der Normalkraft mit dem Betrag der Lastkraft. Für den lastabhängigen Anteil der kinetischen Reibkraft folgt damit

...