1 Einleitung
Mechatronische Systeme zeichnen sich durch ein enges Zusammenwirken mechanischer, elektrotechnischer, hydraulischer und informationstechnischer Komponenten aus. Für die systematische Entwicklung solch komplexer Systeme wird in [1] die nachfolgend beschrie-bene Methodik vorgeschlagen. Nach der Spezifikation der Produktidee und der Produktpla-nung wird mit der Konstruktion begonnen, die sich wiederum in die Konzeptentwicklung, den konstruktiven Entwurf und die Ausarbeitung unterteilen lässt. Im Anschluss an die Konstruk-tion folgt die Realisierung mit der Fertigung der Bauteile und der Montage eines realen Pro-totyps. Schließlich wird das entwickelte System in Labor- und Feldversuchen getestet.
Diese Vorgehensweise ist in großem Maße gestaltorientiert. Bereits nachdem in der Konzep-tentwicklung die Funktionsstruktur und die Lösungsprinzipien ausgearbeitet wurden, wird mit dem konstruktiven Entwurf begonnen. Dabei bleibt häufig das dynamische Verhalten der mechanischen Konstruktion im Zusammenspiel mit anderen Systemkomponenten, wie z.B. Aktoren, Sensoren oder Informationsverarbeitung (Steuerung, Regelung und Signalverarbei-tung), unberücksichtigt. Das dynamische Verhalten des Gesamtsystems kann somit in dieser Entwicklungsphase nicht ermittelt werden. Ob ein entworfenes Systemkonzept die ge-wünschten Ergebnisse liefert, wird erst zu einem viel späteren Zeitpunkt sichtbar. Erst nach Abschluss der Konstruktion und der anschließenden Fertigung und Montage aller Bauteile kann das dynamische Verhalten des Gesamtsystems experimentell analysiert werden. Ergibt sich aus der Analyse, dass Systemkomponenten verändert werden müssen, sind diese in einem zeit- und kostenintensiven Prozess neu zu konstruieren, zu fertigen und schließlich zu montieren. Eine mehrfache Iteration über diese Entwicklungsschritte zur Erzielung eines optimalen Systems ist in Hinblick auf den heutigen Kosten- und Zeitdruck bei der Entwicklung neuer Systeme nicht mehr möglich.
Einen Ausweg bietet in Anlehnung an [2] die Erweiterung der beschriebenen konventionellen Entwicklungsmethodik um den so genannten mechatronischen Entwurf. Der resultierende mechatronische Entwicklungsprozess ist in Bild 1.1 dargestellt.
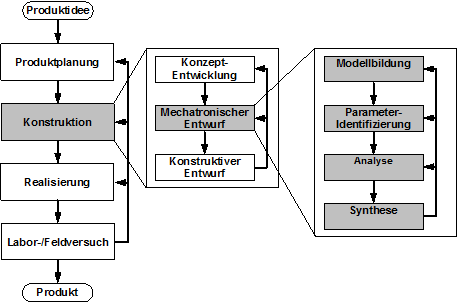
Bild 1.1: Mechatronischer Entwicklungsprozess
Die Vorgehensweise im mechatronischen Entwicklungsprozess ist modellbasiert und verfolgt von Beginn an einen ganzheitlichen Ansatz, der alle Systemkomponenten mit ihrem dynami-schen Verhalten und ihren gegenseitigen Wechselwirkungen bei der Auslegung des Ge-samtsystems berücksichtigt.
Der mechatronische Entwurf beginnt nach der Ausarbeitung eines Systemkonzepts, wobei die konstruktive Ausprägung des Systems zunächst weniger detailliert betrachtet wird. Statt-dessen werden die im konventionellen Entwicklungsprozess zunächst vernachlässigten Komponenten mit ihrem dynamischen Verhalten beim mechatronischen Entwurf berücksich-tigt. Für das Gesamtsystem werden die Stationen Modellbildung, Parameteridentifizierung, Analyse und Synthese (Steuerungs- und Regelungsentwurf) solange rechnergestützt iterativ durchlaufen bis entweder ein ausreichend optimiertes System entwickelt ist oder erkannt wird, dass die gestellten Anforderungen mit dem gewählten Systemkonzept nicht erfüllt wer-den können. Erst nach erfolgreichem Abschluss des mechatronischen Entwurfs wird mit dem detaillierten konstruktiven Entwurf begonnen. Mit dieser Vorgehensweise wird das im Systemkonzept vorhandene Optimierungspotenzial ausgeschöpft und ein in der Realisie-rungsphase aufgebauter realer Prototyp ist schon weitestgehend optimal. Darüber hinaus steht der reale Prototyp schon nach minimaler Entwicklungszeit zur Verfügung.
Während des Durchlaufens der oben genannten Stationen des mechatronischen Entwurfs wird sukzessive ein so genannter virtueller Prototyp des Gesamtsystems in Form eines nichtlinearen parametrischen Simulationsmodells aufgebaut. In dem Simulationsmodell sind die einzelnen Komponenten der mechanischen Tragstruktur, der Aktorik und Sensorik sowie der Steuerung bzw. Regelung und Signalverarbeitung enthalten. Dieses ermöglicht bereits zu einem sehr frühen Zeitpunkt eine hinreichend genaue Nachbildung der Dynamik des Gesamtsystems auf dem Rechner. Mit Hilfe dieses virtuellen Prototyps können verschiedene Optimierungsaufgaben, die sich während des mechatronischen Entwurfs ergeben, durch den Einsatz numerischer Optimierungsverfahren gelöst werden.
Eine wesentliche Aufgabe, die sich während des mechatronischen Entwurfs stellt, ist die in Kapitel 2 dieses Beitrags dargestellte Funktionsoptimierung des Gesamtsystems. Diese hat zum Ziel, noch nicht festgelegte (freie) Systemparameter mit Hilfe des virtuellen Prototyps so zu bestimmen, dass das Verhalten des Gesamtsystems optimal wird.
Nach dem Aufbau und der Inbetriebnahme eines realen Prototyps muss dieser identifiziert werden, um eine gezielte rechnergestützte Weiterentwicklung des betrachteten mechatroni-schen Systems zu ermöglichen. In Kapitel 3 wird eine Vorgehensweise zur Parameteridenti-fizierung beschrieben, die sich ebenfalls auf numerische Optimierungsverfahren stützt.
Eine weitere wichtige Aufgabe im mechatronischen Entwicklungsprozess stellt die Optimie-rung der Steuerung und Regelung eines mechatronischen Systems dar. Diese kann mit Hilfe numerischer Optimierungsverfahren sowohl modellbasiert am virtuellen Prototyp als auch am realen Prototyp erfolgen. Beide Möglichkeiten werden in Kapitel 4 vorgestellt.
Die Verwendung numerischer Optimierungsverfahren ist dabei ohne den Einsatz geeigneter Software-Werkzeuge nicht denkbar. Daher liegt ein Schwerpunkt dieses Beitrags auf der Vorstellung von speziell zugeschnittenen Software-Werkzeugen für die Durchführung von Optimierungsaufgaben. Derartige Software-Werkzeuge sind in Kooperation der DMecS Development of Mechatronic Systems GmbH & Co. KG und dem Labor für Mechatronik der Fachhochschule Köln (Cologne Laboratory of Mechatronics, CLM) als Erweiterung der etab-lierten mechatronischen Entwicklungsumgebung MATLAB/Simulink entwickelt worden. Am Beispiel verschiedener Anwendungen wird die Lösung von Optimierungsaufgaben mit diesen Software-Werkzeugen demonstriert und das Potenzial des systematischen Einsatzes der Optimierung im mechatronischen Entwicklungsprozess dargestellt.
2 Funktionsoptimierung
Als Teil des mechatronischen Entwurfs hat der Prozess der Funktionsoptimierung den Zweck, das Verhalten eines mechatronischen Systems auf Basis des virtuellen Prototyps gezielt zu optimieren. Aufgrund der Komplexität mechatronischer Systeme ist die manuelle Abstimmung der einzelnen Komponenten in Hinblick auf ein optimales Verhalten des Ge-samtsystems kaum möglich. Vielmehr ist zur Lösung dieser Aufgabe der Einsatz von nume-rischen Optimierungsverfahren sinnvoll.
Für die Funktionsoptimierung können auf Basis der Zeitantworten aus der nichtlinearen Simulation des virtuellen Prototyps beliebige Optimierungsaufgaben formuliert und durch gezielte Variation der freien Systemparameter gelöst werden. Freie Systemparameter können z.B. Konstruktionsparameter aber auch Parameter von Steuerung und Regelung sein, wobei letztere nicht zwangsweise als Optimierungsparameter angesehen werden müssen. Statt-dessen können sie nach jeder Variation der freien Systemparameter durch erneuten Steuerungs- und Regelungsentwurf an die veränderten System- bzw. Streckenparameter angepasst werden.
Als Ergebnis liefert die Funktionsoptimierung detaillierte Vorgaben vor allem für die spätere konstruktive Gestaltung. Durch die Verwendung des virtuellen Prototyps als Grundlage für die Optimierung wird die Wechselwirkung der einzelnen Systemkomponenten untereinander berücksichtigt. Zudem kann die im virtuellen Prototyp enthaltene Steuerung, Regelung und Signalverarbeitung bei der späteren Realisierung ohne großen Aufwand für die Inbetrieb-nahme eines gemäß den Ergebnissen aus der Funktionsoptimierung umgesetzten realen Prototyps verwendet werden.
2.1 Verwendung numerischer Optimierungsverfahren für die Funktionsoptimierung
Aus der Vielzahl der für die Funktionsoptimierung anwendbaren Optimierungsverfahren werden in diesem Beitrag numerische Verfahren der Sequentiellen Quadratischen Programmierung (SQP) betrachtet. Für diese Optimierungsverfahren wird eine Optimierungsaufgabe durch eine oder mehrere zu minimierende Zielfunktion(en) und eventuelle Nebenbedingungen formuliert. Zielfunktionen beschreiben das Optimierungsziel mathematisch in Abhängigkeit freier Parameter (Optimierungsparameter). Mit Hilfe von Nebenbedingungen können zusätzliche für die Optimierung zu beachtende Randbedingungen ebenfalls in Abhängigkeit der Optimierungsparameter festgelegt werden. Die Lösung einer Optimierungsaufgabe erfolgt, ausgehend von zuvor manuell bestimmten Startwerten, in einem iterativen Prozess durch systematische Variation der Optimierungsparameter mit Hilfe geeigneter Optimierungsalgorithmen (Parameteroptimierung). Die Parameterwerte, mit denen das Minimum der Zielfunktionen unter Berücksichtigung der Nebenbedingungen beschrieben werden kann, bilden am Ende des Optimierungsprozesses die Lösung der Optimierungsaufgabe. Die genauen theoretischen Hintergründe zu den verwendeten Optimierungsverfahren sollen nicht Bestandteil dieses Beitrags sein. Sie können in [3], [4] oder [5] nachvollzogen werden.
Die für die Funktionsoptimierung eines mechatronischen Systems mit Hilfe eines numerischen Optimierungsverfahrens der SQP gewählte Vorgehensweise ist schematisch in Bild 2.1 dargestellt.
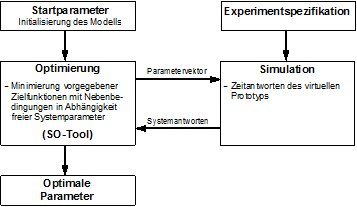
Bild 2.1: Vorgehensweise zur Funktionsoptimierung
Den Ausgangspunkt für die Funktionsoptimierung bilden die Startwerte der freien Systempa-rameter, die aus einem ersten groben Entwurf des betrachteten mechatronischen Systems stammen. Konstruktionsparameter werden zunächst aus Datenblättern, mit Überschlagsfor-meln oder intuitiv festgelegt. Mit den üblichen Entwurfsmethoden der Steuerungs- und Rege-lungstechnik (z.B. Frequenzkennlinien-Verfahren oder LQG-Entwurf) werden unter Verwen-dung von linearisierten Entwurfsmodellen die Parameter der Steuerung und Regelung be-rechnet. Infolge der nur groben Bestimmung enthalten sowohl die Konstruktionsparameter als auch die Steuerungs- und Regelungsparameter häufig noch ein erhebliches Optimie-rungspotenzial.
Eine weitere Grundlage für die Funktionsoptimierung ist die Spezifikation geeigneter Simula-tions-Experimente. Diese müssen so gestaltet sein, dass sie die Abhängigkeit des gesetzten Optimierungsziels von den freien Systemparametern gezielt herausstellen. Des Weiteren ist zu beachten, dass die Funktionsoptimierung zu einem System führt, dass optimal an das gewählte Simulations-Experiment angepasst ist. Das Simulations-Experiment sollte also ein hinreichend großes Spektrum an verschiedenen Betriebszuständen bzw. Betriebsarten des zu optimierenden Systems enthalten.
Für die Optimierung werden aus den Zeitantworten des virtuellen Prototyps, die direkt oder indirekt von den freien Systemparametern abhängig sind, geeignete Zielfunktionen gebildet. Darüber hinaus können Nebenbedingungen formuliert werden, die z.B. bereits bekannten Einschränkungen in der konstruktiven Gestaltung oder Beschränkungen von Größen in der Informationsverarbeitung Rechnung tragen. Der Optimierungsprozess selbst steht in ständiger Wechselwirkung mit der Simulation. Zu jedem Optimierungsschritt, d.h. nach jeder
...