Systematische modellbasierte Schwingungsanalyse einer geregelten elektrischen Servolenkung
VDI/VDE AUTOREG 2017, Berlin, 05.-06. Juli 2017
M. Haßenberg, H. Henrichfreise,
Technische Hochschule Köln
Labor für Mechatronik (Cologne Laboratory of Mechatronics, CLM),
Betzdorfer Str. 2
50679 Köln
info@clm-online.de
www.clm-online.de
H. Briese, T. Schubert,
DMecS Development of Mechatronic Systems GmbH und Co. KG,
Gottfried-Hagen-Straße 20
51105 Köln
info@dmecs.de
www.dmecs.de
G. Wittler,
Hochschule Esslingen
Campus Göppingen,
Robert-Bosch-Straße 1
73037 Göppingen
gerd.wittler@hs-esslingen.de
Kurzfassung
In [1, 2] wurde ein LQG/LTR-Entwurf für die Regelung des Fahrerhandmomentes an elektromechanischen Servolenkungen (Electric Power Steering, EPS) vorgestellt. Auf Grund von beim Reglerentwurf nicht berücksichtigten Elastizitäten in der Lenkmechanik kommt es zu unerwünschten Schwingungen (parasitären Eigenbewegungen). In diesem Beitrag werden die Auswirkungen dieser parasitären Eigenbewegungen auf das Verhalten der Regelung gezeigt. Durch eine detaillierte Modellanalyse werden die Ursachen dieser Probleme verdeutlicht. Die Ergebnisse dieser Modellanalyse werden für einen neuen Regelungsansatz genutzt.
1 Einleitung
Für die Regelung von elektromechanischen Lenksystemen werden unterschiedliche Regelungsalgorithmen eingesetzt. In [1, 2] wurde ein LQG/LTR-Entwurf für die Regelung des Fahrerhandmomentes an EPS-Lenksystemen vorgestellt. Ein Vorteil dieses Regelungsansatzes ist, dass die Einstellung des Lenkgefühls getrennt von dem Entwurf der Regelung durchgeführt wird. Vorrausetzung für die Applikation des Lenkgefühls ist eine robuste Regelung. Aus diesem Grund werden in diesem Beitrag die Robustheitseigenschaften der Regelung genauer betrachtet.
Der bestehende Reglerentwurf berücksichtigt lediglich die Elastizität des Torsionsstabes. In einer elektromechanischen Servolenkung ist jedoch eine Vielzahl weiterer elastischer Lagerungen vorhanden. Diese dienen unter anderem der Geräuschminimierung, dem Ausgleich von Fertigungstoleranzen oder der Minderung von Stößen auf die Lenkmechanik. Da diese Elastizitäten im Reglerentwurf nicht berücksichtigt sind, können sie zu unerwünschten Schwingungen (parasitären Eigenbewegungen) und sogar zu Stabilitätsproblemen führen [3].
Im Rahmen dieses Beitrags wird mit Hilfe eines modellbasierten Ansatzes eine systematische Analyse dieser Schwingungsphänomene beschrieben. Dazu wird in Abschnitt 2 ein detailliertes Modell abgeleitet, das alle in einer Lenkmechanik auftretenden Elastizitäten beinhaltet. Um den Einfluss dieser Elastizitäten auf die Regelung zu untersuchen, wird in Abschnitt 3 die bestehende LQG/LTR-Regelung mit diesem detaillierten Modell analysiert. Die Ursachen der in Abschnitt 3 beschriebenen Probleme werden in Abschnitt 4 durch eine detaillierte Modellanalyse aufgezeigt. Schließlich wird in Abschnitt 5 eine erste Maßnahme zur Verbesserung der Regelung vorgestellt. Die Untersuchungen werden am Beispiel eines achsparallelen EPS durchgeführt. Die Methodik lässt sich grundsätzlich auch auf andere Bauformen übertragen.
2 Modellbildung der Lenkmechanik
Bild 1 zeigt das physikalische Ersatzmodell der Lenkmechanik mit acht Freiheitsgraden (8 DOF). Die einzelnen Körper sind dabei mit den Indizes S (steering), P (pinion), R (rack), N (nut), M (motor), C (casing), V (vehicle), WL (left wheel) und WR (right wheel) versehen. Die Elastizitäten im Modell werden durch die Torsionsstabsteifigkeit ctb (Drehmomentsensor), Flankensteifigkeit des Kugelgewindetriebs cNR , Riemensteifigkeit cMN , Steifigkeit der axialen Mutterlagerung cNC , Steifigkeit der Gehäuseaufhängung cCV und die Steifigkeit der Radanbindung cRW berücksichtigt. Die Trägheiten, bzw. Massen der Körper werden mit JX , bzw. mit mX bezeichnet, wobei der Index den entsprechenden Körper darstellt. Übersetzungsverhältnisse sind mit iXY bezeichnet, wobei der erste Index für den antreibenden Körper und der zweite Index für den angetriebenen Körper steht.
Für das dargestellte physikalische Ersatzmodell wurden die Bewegungsgleichungen hergeleitet, für die Analyse linearisiert und in Zustandsraumdarstellung überführt. Ausgehend von dem Modell mit acht Freiheitsgraden wurde durch eine physikalisch motivierte Modellreduktion ein weiteres Modell mit drei Freiheitsgraden (3 DOF) erzeugt.
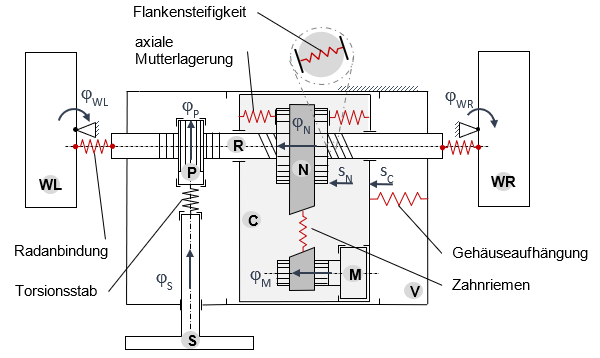
Bild 1 Physikalisches Ersatzmodell der Lenkmechanik mit acht Freiheitsgraden
Wird nur die Torsionsstabsteifigkeit berücksichtigt und werden die übrigen Verbindungen als starr angenommen, können die Trägheiten der Körper M, N, R, P, WL und WR zusammengefasst werden. Aus diesem Schritt resultiert das Modell mit zwei Freiheitsgraden (2 DOF) aus [1,2].
Die verschiedenen Modelle für die Lenkmechanik werden jeweils um ein Modell eines stromgeregelten EPS-Motors erweitert und bilden mit diesem das Modell der Regelstrecke.
2.1 Prüfstandregelung
Die Nachbildung der realen Betriebsumgebung des EPS-Motors wird durch eine hochdynamische Regelung der Lastmaschine des Powerpack-Prüfstands erreicht. Die hierzu verwendete Regelung wird als Prüfstandsregelung bezeichnet und stellt als Regelgröße eine Schnittgröße an der Welle des EPS-Motors ein. Als Schnittgröße wird, u.a. abhängig von der HiL-Anwendung, entweder die Lage, die Winkelgeschwindigkeit oder das Moment am EPS-Motor verwendet.
Neben einer hohen Regelungsbandbreite ist eine hohe Regelgenauigkeit erforderlich. Dies muss trotz Störungen wie Reibung, Drehmomentwelligkeit und Messrauschen realisiert werden. Etwaige Eigenschwingungen des Prüfstandssystems können durch die Prüfstandsregelung aktiv gedämpft werden.
Um diese Ziele zu erreichen, ist die Prüfstandsregelung als beobachterbasierter Zustandsregler [1] implementiert. Zudem wird die Regelgüte durch ein nichtlineares Modell zur Kompensation der Momentenwelligkeit der Lastmaschine verbessert.
3 Regelungssystem mit verschiedenen Modellen für Lenkmechanik
Das Bild 2 zeigt das Regelungssystem bestehend aus dem dynamischen LQG-Kompensator und dem Modell der Regelstrecke. Als Kompensator wird hier die Zusammenschaltung eines optimalen Zustandsreglers (LQR) und eines optimalen Zustandsbeobachters (LQE) bezeichnet.
...
